力扣-3-无重复字符的最长子串（Longest Substring Without Repeating Characters）

最后编辑于2025-5-20

3. 无重复字符的最长子串（Longest Substring Without Repeating Characters）

中等

给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。

示例 1：

输入： s = “abcabcbb”
输出： 3
解释： 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2：

输入： s = “bbbbb”
输出： 1
解释： 因为无重复字符的最长子串是 “b”，所以其长度为 1。

示例 3：

输入： s = “pwwkew”
输出： 3
解释： 因为无重复字符的最长子串是 “wke”，所以其长度为 3，注意答案必须是子串长度。

提示：

  • 0 <= s.length <= 5 * 10^4
  • s 由英文字母、数字、符号和空格组成

方法一：暴力枚举

思路：
从字符串的每一个起始位置出发，依次向后扩展子串，同时使用一个布尔数组或集合来记录当前子串中出现过的字符，一旦遇到重复字符，则停止扩展，对比记录最长长度。该方法直观易懂，但效率较低。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int n = s.size(), ans = 0;
        for (int i = 0; i < n; ++i) {
            vector<bool> seen(256, false);
            int len = 0;
            for (int j = i; j < n; ++j) {
                if (seen[(unsigned char)s[j]]) break;
                seen[(unsigned char)s[j]] = true;
                ++len;
            }
            ans = max(ans, len);
        }
        return ans;
    }
};
  • 时间复杂度： O(n^3)
  • 空间复杂度： O(1)

方法二：滑动窗口

思路：
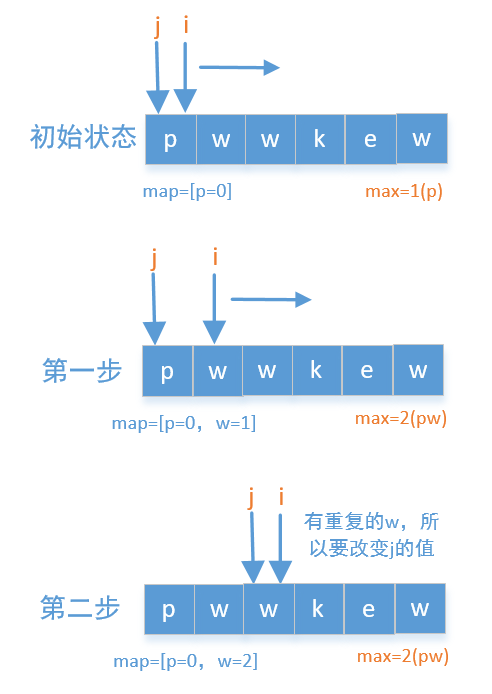
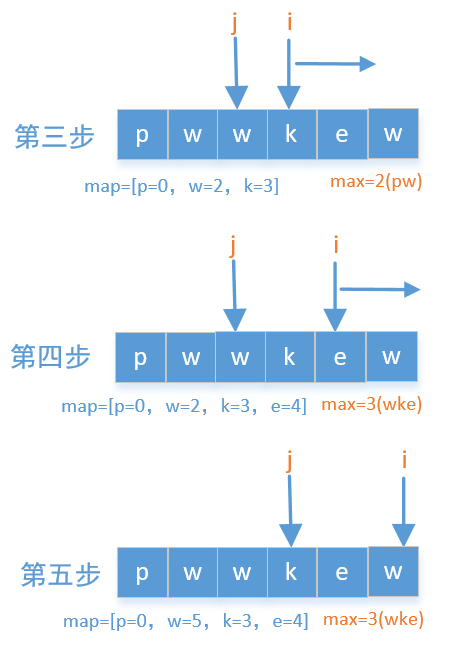
维护一个滑动窗口，用两个指针 l(图中为j)（左边界）和 r(图中为i)（右边界），以及一个哈希数组记录窗口内字符出现次数。当右指针包含的新字符导致重复时，就移动左指针并更新计数，直到窗口中不再有重复字符，同时每次都更新最大窗口长度。

图1
图2

  • 以上两图来自力扣题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        vector<int> count(128, 0);
        int ans = 0, l = 0;
        for (int r = 0; r < s.size(); ++r) {
            ++count[s[r]];
            while (count[s[r]] > 1) {
                --count[s[l]];
                ++l;
            }
            ans = max(ans, r - l + 1);
        }
        return ans;
    }
};
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

方法三：优化滑动窗口（记录上次出现位置）

思路：
使用数组 lastSeen 记录每个字符上次出现的索引，当遍历到字符 s[i] 时，若 lastSeen[s[i]] 在当前窗口内，则直接将左边界 start 移动到 lastSeen[s[i]] + 1，这样无需逐步移动指针，窗口始终保持无重复状态，同时更新最长长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        vector<int> lastSeen(128, -1);
        int ans = 0, start = 0;
        for (int i = 0; i < s.size(); ++i) {
            start = max(start, lastSeen[(unsigned char)s[i]] + 1);
            ans = max(ans, i - start + 1);
            lastSeen[(unsigned char)s[i]] = i;
        }
        return ans;
    }
};
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

算法性能与系统原理

在实际工程中，算法的运行速度与空间占用不仅取决于算法复杂度，还深受底层系统架构、缓存局部性和内存分配策略的影响。

  1. 缓存命中率（Cache Locality）：

    • 方法一每次内层循环都重置布尔数组，随机访问计数，导致CPU缓存难以复用，缓存未命中率高，实际运行速度远低于理论复杂度。
    • 方法二与方法三使用连续数组存储字符计数或上次出现位置，读取和写入集中在数组局部，具有良好的缓存局部性，缓存命中率高，实际性能优越。

  2. 分支预测与流水线：

    • while (count[s[r]] > 1)等条件分支会影响CPU流水线。方法二中的循环分支较多，而方法三通过直接计算新边界减少了条件判断次数，分支更容易预测，流水线停顿更少。

  3. 内存占用和频繁分配：

    • 方法一每次迭代都开辟新 vector<bool> 或集合，触发频繁内存分配和释放；
    • 方法二与方法三只初始化一次数组，重用内存，减少分配开销。

案例教程：滑动窗口算法实战

以方法二为例，逐步解析运行过程： 

1
2
3
4
5
6
7
8
9
输入 s = "abca"
初始化: count['a']=0,count['b']=0,... l=0, ans=0
r=0: s[0]='a' -> count['a']++ => 1, ans=max(0,1)=1
r=1: s[1]='b' -> count['b']++ => 1, ans=max(1,2)=2
r=2: s[2]='c' -> count['c']++ => 1, ans=max(2,3)=3
r=3: s[3]='a' -> count['a']++ => 2 -> 重复，进入 while:
    l=0 -> count['a']-- =>1, l=1 -> 退出 while，窗口 = [1,3]
更新 ans=max(3,3)=3
最终返回 3

流程图

方法二：滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
+---------------------+
| start l=0, r遍历至n |
+----------+----------+
           |
           v
    +------v-------+
    | count[s[r]]++ |
    +------+-------+
           |
           v
    +------v-------+
    | count>1 ?    |--是--> [-- l移动, count[s[l]]--, goto判断 --]
    |             |  否
    +------+-------+
           |
           v
    +------v-------+
    | 更新 ans     |
    +------+-------+
           |
           v
    +------v-------+
    | r++ 继续     |
    +--------------+

方法三：优化滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
+-------------------------+
| 初始化 start=0, lastSeen=-1 |
+----------+--------------+
           |
           v
    +------v-------+
    | 遍历 i from 0|
    +------+-------+
           |
           v
    +------v-------+
    | 新start = max(start, lastSeen[s[i]]+1) |
    +------+-------+
           |
           v
    +------v-------+
    | 更新 ans = max(ans, i-start+1)         |
    +------+-------+
           |
           v
    +------v-------+
    | lastSeen[s[i]] = i                    |
    +------+-------+
           |
           v
    +------v-------+
    | i++ 继续                               |
    +--------------+

相关建议与扩展

  • 代码优化： 在C++中，可以使用 array<int, 256> 替代 vector 以进一步提高性能。
  • Unicode 支持： 若字符串包含宽字符（如中文），需使用 unordered_map<char32_t,int> 或者对UTF-8字节流逐字节处理。
  • 在线测试： 在多组测试用例下测量执行时间，可使用谷歌Benchmark库评估微观性能。

作者想说的话：

这道题是字符串滑动窗口的经典示例，推荐掌握方法三作为最佳方案。

更多字符串变体练习：