力扣-1.两数之和（Two Sum）

最后编辑于2025-5-18

1. 两数之和（Two Sum）

简单

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。

示例 1：

输入： nums = [2,7,11,15], target = 9
输出： [0,1]
解释： 因为 nums[0] + nums[1] == 9，返回 [0, 1]。

示例 2：

输入： nums = [3,2,4], target = 6
输出： [1,2]

示例 3：

输入： nums = [3,3], target = 6
输出： [0,1]

提示：

  • 2 <= nums.length <= 10^4
  • -10^9 <= nums[i] <= 10^9
  • -10^9 <= target <= 10^9
  • 只会存在一个有效答案

进阶：

你可以想出一个时间复杂度小于 O(n^2) 的算法吗？

方法一：暴力枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return {i, j};
                }
            }
        }
        return {};
    }
};
  • 执行用时： 47ms，击败 28.79%
  • 内存消耗： 13.80MB，击败 83.42%

思路：
嵌套两个循环，枚举数组中每一对 (i, j)，检查 nums[i] + nums[j] == target 时立即返回下标。不使用额外空间，直观易实现，但在 n 较大时性能迅速下降。

流程图： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
┌───────────┐
│ Start     │
└─────┬─────┘
      │ i=0, j=1
┌─────▼─────┐
│ Check sum │
│ nums[i]+  │
│ nums[j]   │
└─────┬─────┘
      │ == target?
 ┌────▼────┐      ┌───────────┐
 │ Yes     │────▶│ Return    │
 │         │      │ {i, j}    │
 └────▲────┘      └───────────┘
      │ No
┌─────▼─────┐
│ j++ or    │
│ i++, reset│
└─────┬─────┘
      │ Continue
      ▼
    End loop

方法二：二次遍历哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> lookup;
        int n = nums.size();
        // 第一次遍历：填表
        for (int i = 0; i < n; ++i) {
            lookup[nums[i]] = i;
        }
        // 第二次遍历：找补数
        for (int i = 0; i < n; ++i) {
            int c = target - nums[i];
            auto it = lookup.find(c);
            if (it != lookup.end() && it->second != i) {
                return {i, it->second};
            }
        }
        return {};
    }
};
  • 执行用时： 7ms，击败 43.89%
  • 内存消耗： 15.74MB，击败 5.38%

思路：
利用哈希表在 O(1) 平均时间内完成查找。第一次遍历将元素值映射到下标，第二次遍历寻找补数并验证。

流程图： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
┌───────────┐
│ Start     │
└─────┬─────┘
      │ i=0
┌─────▼─────┐
│ Fill map  │
│ lookup[   │
│ nums[i]]=i│
└─────┬─────┘
      │ i<n?
 ┌────▼────┐      ┌────────┐
 │ Yes     │────▶│Continue│
 └────▲────┘      └────────┘
      │ No
┌─────▼─────┐
│ j=0       │
└─────┬─────┘
      │
┌─────▼─────┐
│ Find c    │
│ c=target- │
│ nums[j]   │
└─────┬─────┘
      │ found?
┌─────▼─────┐      ┌────────┐
│ Yes       │────▶│ Return │
│           │      │ {j,it }│
└─────┬─────┘      └────────┘
      │ No
      ▼
    j++, loop

方法三：一次遍历哈希表（相对最优解）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <vector>
#include <unordered_map>
using namespace std;

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> lookup;              // 准备一个空的哈希表
        for (int i = 0; i < (int)nums.size(); ++i) { // 遍历每个元素
            int complement = target - nums[i];       // 计算补数
            auto it = lookup.find(complement);       // 在哈希表中查找补数
            if (it != lookup.end()) {               // 若找到了
                return {it->second, i};              // 立即返回“补数的下标 + 当前下标”
            }
            lookup[nums[i]] = i;                     // 否则，将当前元素插入哈希表
        }
        return {};
    }
};
  • 执行用时： 0ms，击败 100.00%
  • 内存消耗： 14.55MB，击败 45.96%

思路：
在同一次遍历中完成查找与插入操作，边遍历边搜索，降低了常数开销，是最优实践。

流程图： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
┌────────────┐
│ Start      │
└──────┬─────┘
       │ i=0
┌──────▼─────┐
│ Compute    │
│ complement │
└──────┬─────┘
       │ lookup.find?
┌──────▼─────┐      ┌──────────┐
│ Found?     │────▶│ Return   │
│ it!=end    │      │ {pos,i}  │
└──────┬─────┘      └──────────┘
       │ No
┌──────▼─────┐
│ Insert num │
│ lookup[val]│
└──────┬─────┘
       │ Continue
       ▼
     End loop

算法原理与性能分析

  1. 计算机层面运行原理

    • CPU 指令流水线：在暴力枚举中，分支预测失误成本高，频繁分支跳转导致流水线清空，降低执行效率。哈希查找中分支少，流水线利用率更高。
    • 缓存（Cache）命中：暴力枚举随机访问数组元素，缓存命中率较低；哈希表操作也有随机访问，但现代 CPU L1/L2 缓存可加速哈希桶的访问。
    • 内存分配与扩展：哈希表在增长时需要重新分配和再哈希，开销为 O(n)，但摊销到每次插入时均摊为 O(1)。

  2. 时间复杂度分析

    • 暴力枚举：O(n²)，随着 n 增大，运算量急剧上升。
    • 二次遍历哈希：O(n) + O(n) = O(n)，额外遍历构建和查找。
    • 一次遍历哈希：O(n) 平均，最坏 O(n²)（所有元素哈希冲突时）。

  3. 空间复杂度分析

    • 暴力枚举：O(1)，无额外存储。
    • 哈希表方法：O(n)，需存储 n 个键值对。
    • 空间换时间策略：在内存充足时，优先考虑哈希方法。

  4. 实践建议

    • 对于小规模数组（n < 1000），暴力枚举也能在毫秒级完成。
    • 对于大规模数据，推荐一次遍历哈希，保证线性性能。
    • 若内存敏感，可考虑空间占用更小的排序加双指针方案，但不适用于无序数组的索引返回。

教程与扩展

  1. 详细步骤

    • 理解题意：需要返回下标，对数组进行两两组合或查找补数。
    • 选择合适的数据结构：哈希表对于查找补数是最合适的。
    • 编码实现：注意边界条件与哈希冲突。
    • 测试用例：考虑正负数、重复元素、目标值为 0 等。

  2. 可视化教程

    线性探测插入流程详解

哈希表插入示例

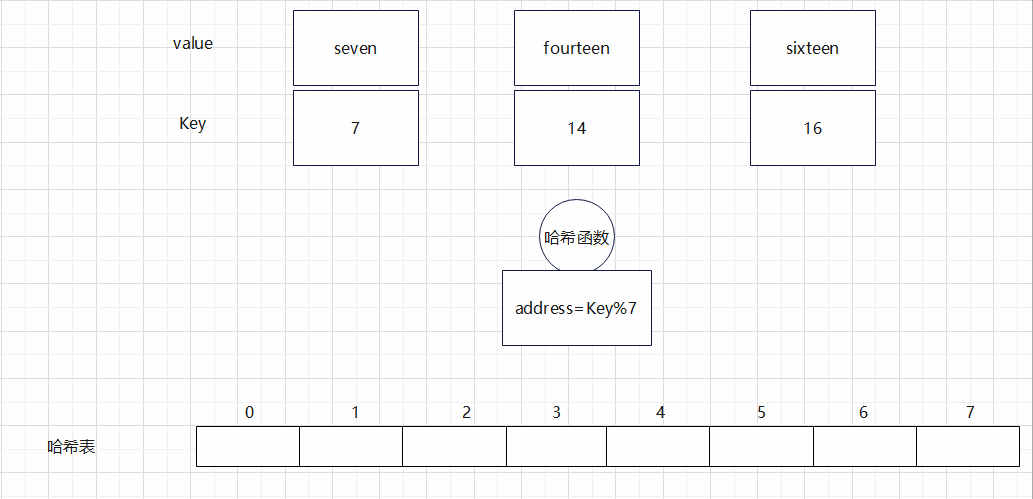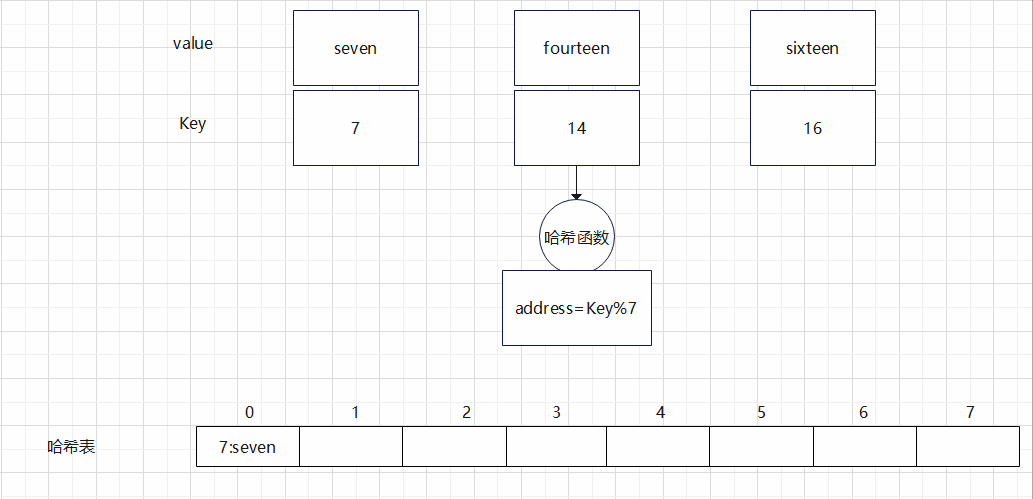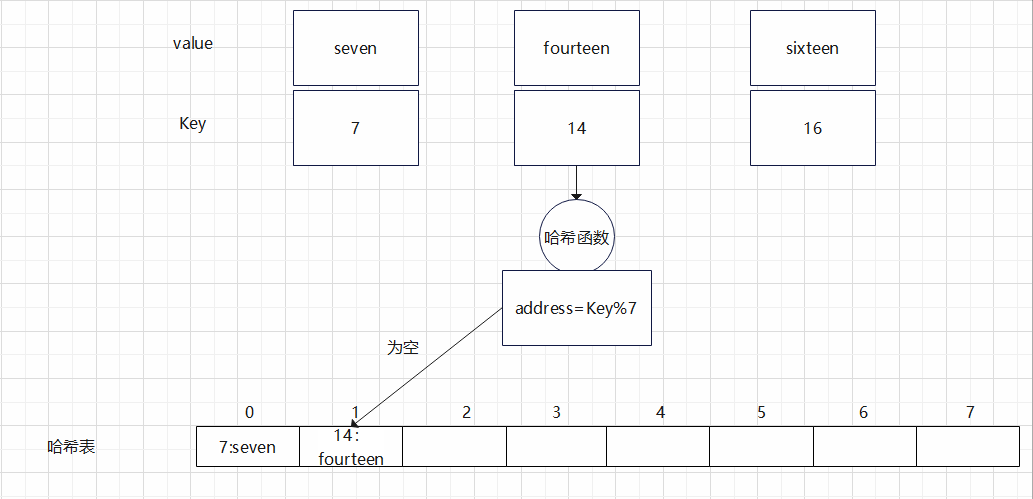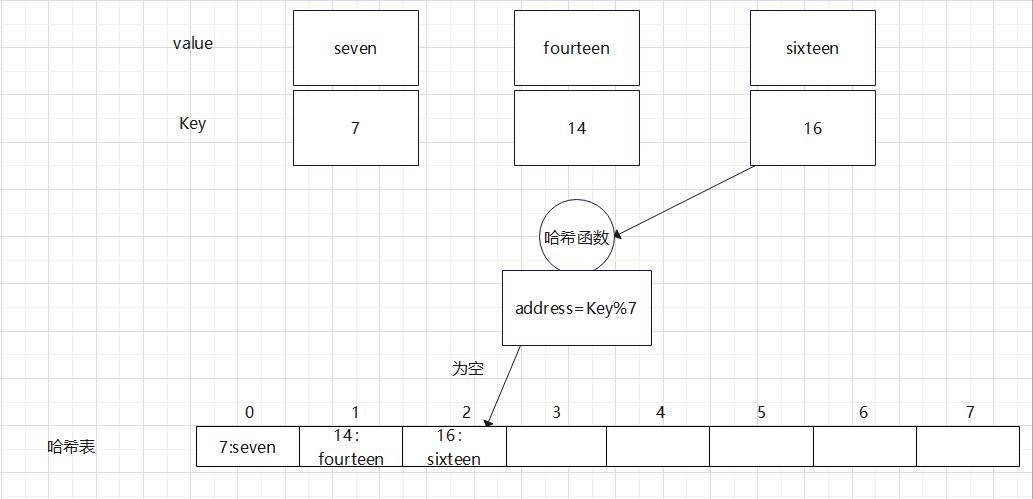
① 插入第一个元素

  • 将键值对 (7, "seven") 准备插入哈希表。
  • 通过哈希函数计算，得到目标下标为 0。
  • 检查哈希表索引 0 处，当前为空槽，所以直接在此位置存放 (7, "seven")。

② 插入第二个元素

  • 将键值对 (14, "fourteen") 准备插入哈希表。
  • 经过同样的哈希映射，也得到下标 0。
  • 发现位置 0 已被占用，需要寻找下一个可用槽。

③ 线性探测寻址

  • 从冲突下标 0 开始，依次往后探查：
    1. 检查下标 1，若为空则将 (14, "fourteen") 存入；
    2. 若下标 1 也已占用，则继续检查下标 2、3……
  • 直到遇到第一个空槽，将该键值对存储于此。

说明：

  • 本示例采用“线性探测”（Linear Probing）法来处理哈希冲突；
  • 如果探测到数组末尾仍未找到空槽，可认为哈希表已满，或采取环绕回到数组开头的方式继续探测。

实践练习

作者想说的话：
“两数之和（Two Sum）” 是经典入门题，这三种解法体现了解题思路的演进。深入理解算法底层原理，有助于在面试和工程实践中快速做出最佳选择。